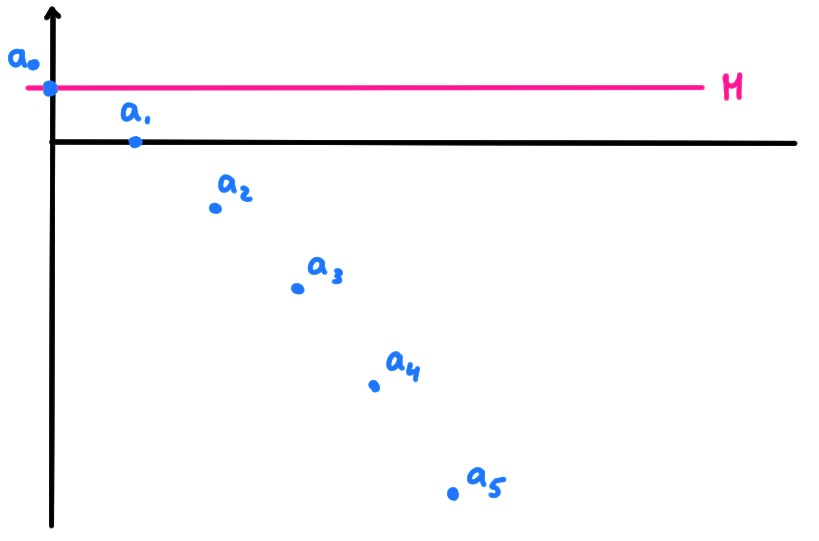
La façon la plus simple est de la représenter simplement comme un ensemble de points sur la droite, \(\{a_1,a_2,\dots\}\subset \mathbb{R}\):
Une suite peut commencer par un indice \(n_0\) quelconque, mais le plus souvent on considérera \(n_0=0\) ou \(n_0=1\). Quand le premier indice n'importe pas ou peu (ce qui sera le cas lorsqu'on étudiera le comportement de \(a_n\) pour des indices \(n\) grands), on écrira parfois \((a_n)\) au lieu de \((a_n)_{n\geqslant n_0}\).
On se représente en général une suite \((a_n)_{n\geqslant 1}\) de deux façons.
La façon la plus simple est de la représenter simplement comme un ensemble de points sur la droite, \(\{a_1,a_2,\dots\}\subset \mathbb{R}\):
Du fait que cet ensemble est ordonné, cette image peut aussi s'interpréter comme une trajectoire: une particule est au point \(a_1\) au temps \(n=1\), puis au point \(a_2\) au temps \(n=2\), etc.
Mais une façon plus intuitive de se représenter une suite est de la voir comme le graphe d'une fonction \[\begin{aligned} f:\mathbb{N}^*&\to\mathbb{R}\\ n&\mapsto f(n):= a_n\,. \end{aligned}\] Ceci revient à représenter les paires de points \((n,f(n))=(n,a_n)\) dans le plan cartésien:
Souvent, une suite est définie simplement en disant comment le \(n\)-ème terme \(a_n\) se calcule explicitement en fonction de l'indice \(n\). Lorsqu'une suite est définie ainsi, chaque terme peut être calculé directement, indépendamment des autres, à l'aide d'une formule.
Exemple: Soit \((a_n)_{n\geqslant 1}\) la suite définie ainsi: pour chaque \(n\geqslant 1\), \[ a_n=\frac{3n^3+n-5}{5n^2+7}\,. \] Dans cet exemple, \(a_{10'000}\) peut se calculer directement, sans avoir forcément besoin de calculer les autres.
Exemple: Soit \((a_n)_{n\geqslant 0}\), définie ainsi: \(a_0=\frac{1}{3}\), puis pour tout \(n\geqslant 1\), \[ a_n=4a_{n-1}(1-a_{n-1})\,. \] Cette suite est définie par récurrence: à part le premier, chaque terme est défini en fonction du précédent. Donc on ne peut calculer \(a_{10'000}\) que si on a déjà calculé \(a_{9'999}\), \(a_{9'998}\), etc. Ce type de suite sera étudié dans un chapitre à part.
On peut définir une suite de façon tout à fait arbitraire, ce qui mène rapidement à des suites difficiles à étudier:
Exemple: Considérons l'expansion décimale du nombre \(\pi\), \[ \pi=3.1415926535897932384626433\dots, \] et définissons la suite \((a_n)_{n\geqslant 1}\), comme suit: \[ a_1=1\,,\quad a_2=4\,,\quad a_3=1\,,\quad a_4=5\,,\quad a_5=9\,,\quad a_6=2\,,\quad\dots \] Plus précisément: \(a_n\) est l'entier représentant le \(n\)-ème chiffre après la virgule dans l'expansion décimale de \(\pi\). Une suite facile à définir, mais très difficile à étudier...
Une propriété simplificatrice, pour une suite, est que ses termes ne soient globalement pas trop grands:
Exemple: Considérons la suite \[a_n=1-n^2\,,\qquad n\geqslant 0\,. \] Alors \((a_n)_{n\geqslant 0}\) est majorée. En effet, \(n^2\geqslant 0\) pour tout \(n\), et donc \[a_n=1-n^2\leqslant 1\,,\qquad \forall n\geqslant 0\,.\] et donc en prenant \(M=1\), on a \(a_n\leqslant M\) pour tout \(n\).
Par contre, \(a_n\) n'est pas minorée (et donc pas bornée). En effet, montrons que pour toute constante \(m\), il existe un indice \(n\) tel que \(a_n\lt m\). Ceci est vrai lorsque \(m\geqslant 0\) puisque \(a_n\leqslant 0\) dès que \(n\geqslant 1\). Si maintenant \(m\lt 0\), alors \(a_n=1-n^2\lt m\) si et seulement si \(n\gt\sqrt{1-m}\) (on a simplement résolu l'inéquation). Donc en prenant n'importe quel entier \(n\) plus grand que \(\sqrt{1-m}\), on a bien que \(a_n\lt m\). Ceci montre qu'il n'existe aucun minorant pour cette suite.
Exemple:
Considérons la suite \[a_n=2\sin(5n+1)-3\cos(\sqrt{n})\,,\qquad n\geqslant 0\,.\] Puisque \[\begin{aligned} |a_n| &=\big|2\sin(5n+1)-3\cos(\sqrt{n})\big|\\ &\leqslant|2\sin(5n+1)|+|-3\cos(\sqrt{n})|\\ &= 2|\sin(5n+1)|+3|\cos(\sqrt{n})|\\ &\leqslant 2+3=5\,, \end{aligned}\] la suite est bornée: \[ -5\leqslant a_n\leqslant +5\,,\qquad \forall n\,. \]
Exemple: La suite \((a_n)_{n\geqslant 1}\), où \(a_n:= n\)ème chiffre de l'expansion décimale de \(\pi\) en base \(10\), est bornée, car minorée par \(0\), et majorée par \(9\).
Exemple: La suite \(a_n=(-1)^nn\) n'est pas majorée. En effet, fixons un seuil \(M\gt 0\) (sous-entendu: aussi grand que l'on veut), et prenons un entier pair \(n=2k\) quelconque, tel que \(k\gt M/2\). On a alors \[ a_n=a_{2k}=(-1)^{2k}2k=2k\gt M\,.\] Cette suite n'est pas minorée non plus. En effet, fixons un seuil \(m<0\) (sous-entendu: aussi grand que l'on veut, négatif), et prenons un entier impair \(n=2k+1\) quelconque, tel que \(k\gt -(m-1)/2\). On a alors \[ a_n=a_{2k+1}=(-1)^{2k+1}(2k+1)=-(2k+1)\lt m\,.\]
Exemple: La suite \(a_n=n^2\), \(n\geqslant 0\), est strictement croissante puisque \[ a_{n+1}=(n+1)^2=n^2+\underbrace{2n+1}_{\gt 0}\gt n^2=a_n\,. \]
Exemple: La suite harmonique \(a_n=\frac{1}{n}\), \(n\geqslant 1\), est strictement décroissante puisque \[ a_{n+1}=\frac{1}{n+1}\lt \frac1n=a_n \]
Les résultats que nous allons présenter dans les prochaines sections au sujet des suites seront d'importance capitale pour toute la suite de ce cours. En effet, l'étude des suites représente la porte d'entrée par laquelle plusieurs des difficultés de l'analyse sont abordées, de façon aussi élémentaire que possible. En particulier, on y discutera pour la première fois de la notion de limite, dans la section suivante, notion essentielle dans l'étude d'une fonction au voisinage d'un point.
Dernière compilation: 2025-08-07 (07:09:50)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
